A. Pengertian Teorema Pythagoras
Teorema Pythagoras menyatakan hubungan antara sisi-sisi segitiga siku-siku. Bunyinya:
"Pada segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang sisi-sisi penyikunya."
Secara matematis:
= sisi miring (hipotenusa)
dan = sisi penyiku (sisi siku-siku)
Contoh Gambar:
Pada ∆ABC siku-siku di B:
Sisi di depan sudut siku-siku (AC) = sisi miring ()
AB () dan BC () = sisi penyiku
B. Rumus Pythagoras dan Penerapannya
Mencari Sisi Miring
Mencari Sisi Penyiku
Contoh Soal 1:
Diketahui segitiga siku-siku dengan sisi penyiku 6 cm dan 8 cm. Hitung panjang sisi miringnya!
Pembahasan:
Contoh Soal 2:
Sebuah segitiga siku-siku memiliki sisi miring 13 cm dan salah satu sisi penyiku 5 cm. Tentukan panjang sisi penyiku lainnya!
Pembahasan:
C. Tripel Pythagoras
Tripel Pythagoras adalah kelompok tiga bilangan bulat positif yang memenuhi teorema Pythagoras. Contoh:
3, 4, 5 →
5, 12, 13 →
7, 24, 25 →
Catatan: Kelipatan tripel juga termasuk tripel Pythagoras. Contoh: 6, 8, 10 (kelipatan 2 dari 3, 4, 5).
D. Penerapan dalam Soal Cerita
Contoh Soal 3:
Seorang anak menerbangkan layang-layang dengan benang sepanjang 15 m. Jarak anak ke titik tepat di bawah layang-layang adalah 9 m. Berapa ketinggian layang-layang?
Pembahasan:
Benang = sisi miring ()
Jarak horizontal = sisi penyiku ()
Tinggi layang-layang ():
E. Latihan Soal
Diketahui segitiga PQR siku-siku di Q. Jika PQ = 5 cm dan QR = 12 cm, hitung PR!
Sebuah tangga panjangnya 10 m bersandar pada tembok. Jika jarak kaki tangga ke tembok 6 m, berapa tinggi tembok yang dicapai tangga?
Tentukan jenis segitiga dengan panjang sisi: 7 cm, 8 cm, 11 cm!
Apakah 8, 15, 17 termasuk tripel Pythagoras? Buktikan!
Hitung panjang diagonal persegi panjang dengan panjang 12 cm dan lebar 9 cm!
Kunci Jawaban:
Tinggi tembok = 8 m
Segitiga tumpul (karena )
Ya, karena
Diagonal = 15 cm
Subscribe by Email
Follow Updates Articles from This Blog via Email



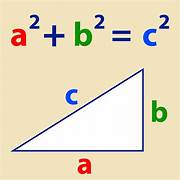
No Comments